Car Accidents Analysis

Q1: Car accident dataset

Q1.1

# Glimpse at the data
glimpse(accident_data)

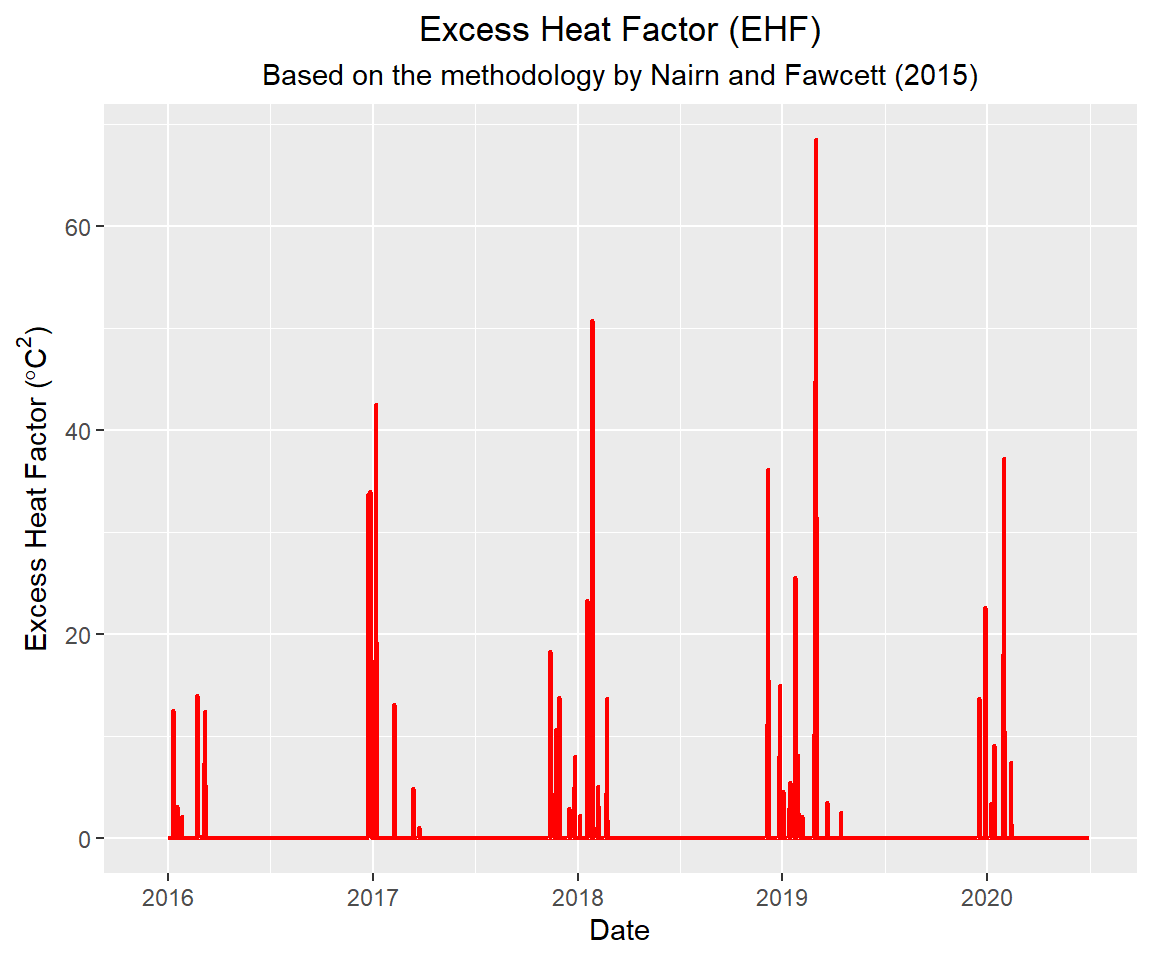
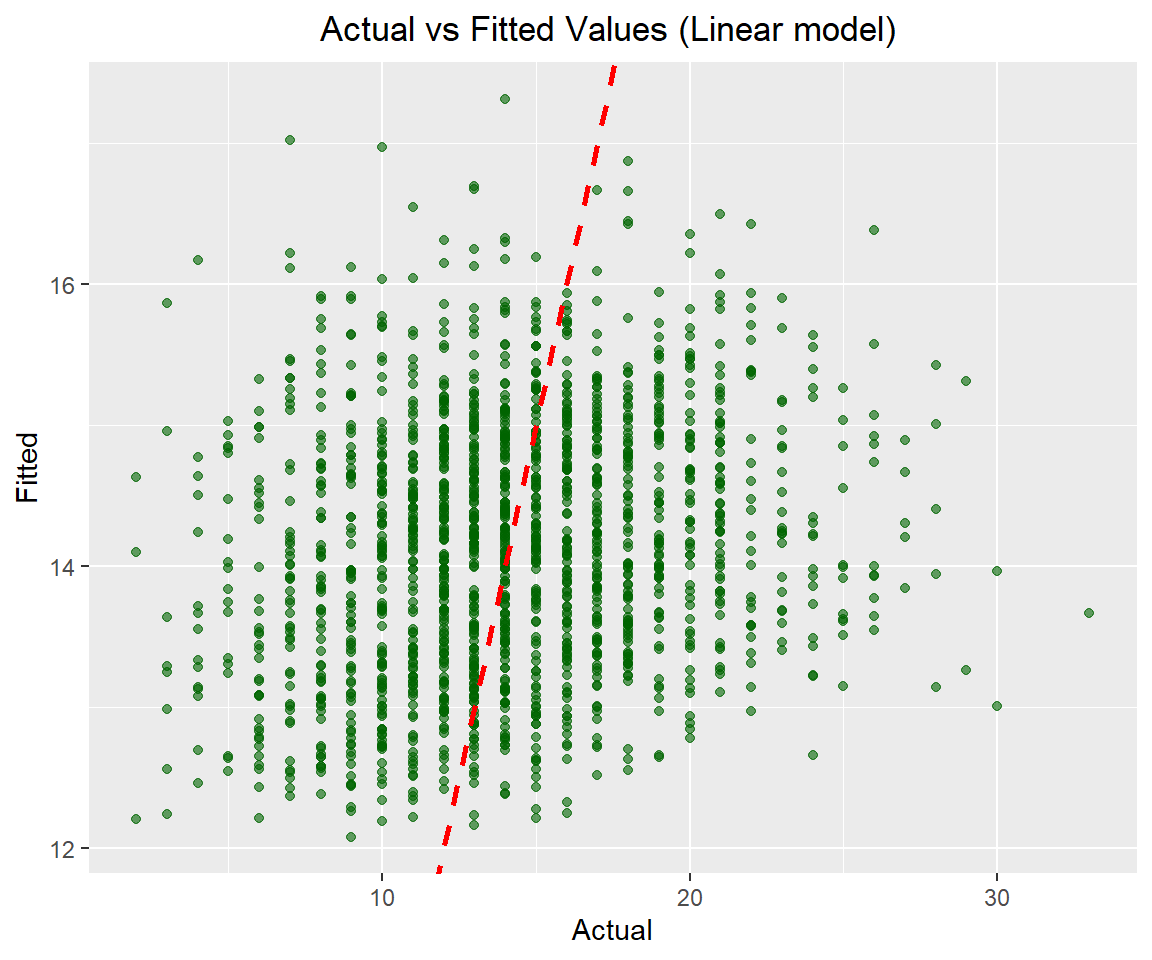
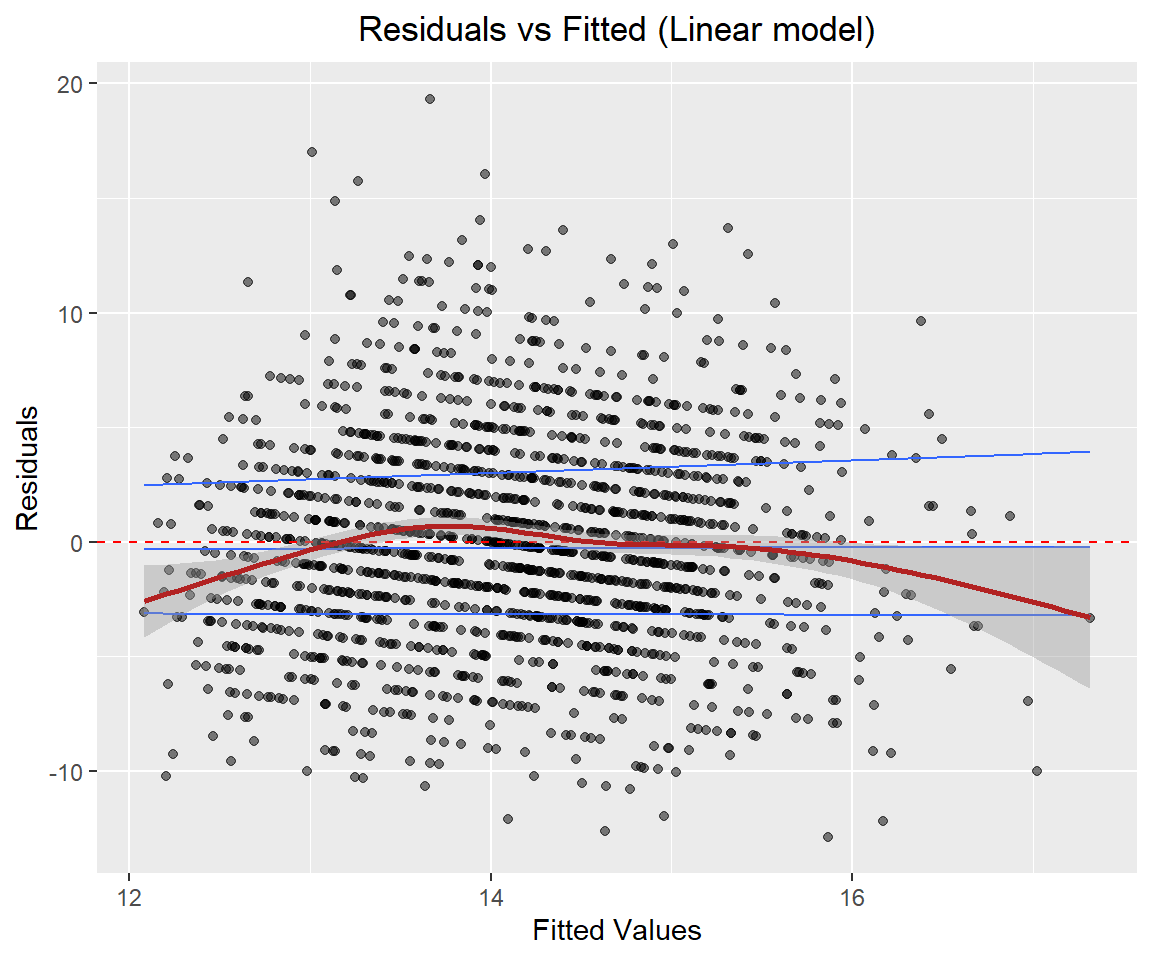
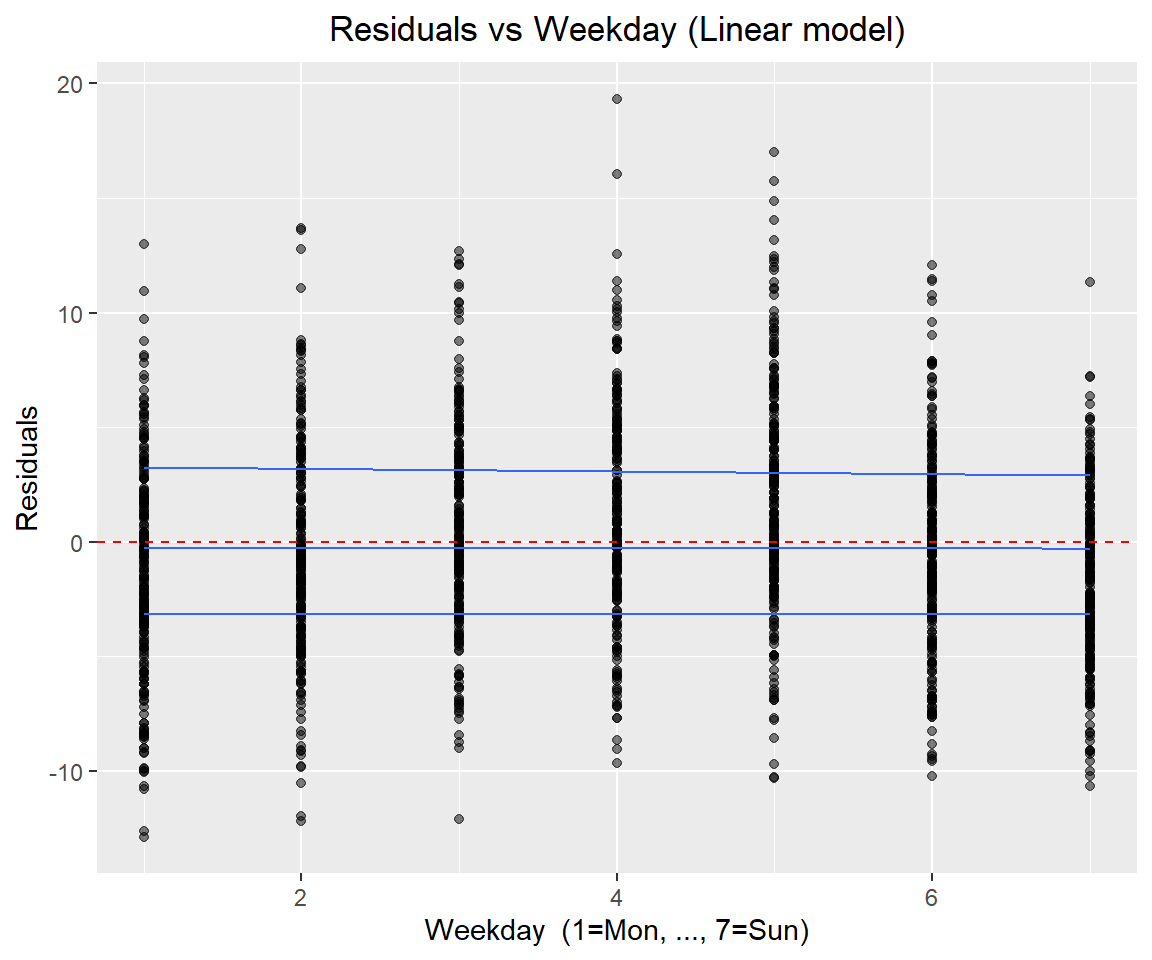
Rows: 1,644
Columns: 29
$ X                              <chr> "DATE", "1/01/2016", "2/01/2016", "3/01…
$ EASTERN.REGION                 <chr> "FATAL", "0", "0", "0", "0", "0", "0", …
$ X.1                            <chr> "SERIOUS", "1", "3", "1", "2", "1", "2"…
$ X.2                            <chr> "NOINJURY", "0", "0", "0", "0", "0", "0…
$ X.3                            <chr> "OTHER", "5", "1", "5", "2", "6", "1", …
$ METROPOLITAN.NORTH.WEST.REGION <chr> "FATAL", "0", "0", "0", "0", "1", "0", …
$ X.4                            <chr> "SERIOUS", "7", "2", "3", "2", "2", "5"…
$ X.5                            <chr> "NOINJURY", "0", "0", "0", "0", "0", "0…
$ X.6                            <chr> "OTHER", "7", "4", "6", "5", "7", "13",…
$ METROPOLITAN.SOUTH.EAST.REGION <chr> "FATAL", "1", "0", "0", "0", "0", "0", …
$ X.7                            <chr> "SERIOUS", "9", "8", "7", "4", "6", "7"…
$ X.8                            <chr> "NOINJURY", "0", "0", "0", "0", "0", "0…
$ X.9                            <chr> "OTHER", "3", "5", "4", "5", "7", "8", …
$ NORTH.EASTERN.REGION           <chr> "FATAL", "0", "1", "0", "0", "0", "0", …
$ X.10                           <chr> "SERIOUS", "3", "2", "2", "1", "6", "0"…
$ X.11                           <chr> "NOINJURY", "0", "0", "0", "0", "0", "0…
$ X.12                           <chr> "OTHER", "2", "1", "3", "1", "2", "0", …
$ NORTHERN.REGION                <chr> "FATAL", "0", "0", "0", "1", "0", "0", …
$ X.13                           <chr> "SERIOUS", "1", "2", "0", "4", "0", "3"…
$ X.14                           <chr> "NOINJURY", "0", "0", "0", "0", "0", "0…
$ X.15                           <chr> "OTHER", "1", "1", "3", "3", "3", "4", …
$ SOUTH.WESTERN.REGION           <chr> "FATAL", "0", "0", "0", "0", "0", "0", …
$ X.16                           <chr> "SERIOUS", "2", "2", "2", "1", "3", "1"…
$ X.17                           <chr> "NOINJURY", "0", "0", "0", "0", "0", "0…
$ X.18                           <chr> "OTHER", "0", "2", "1", "3", "1", "3", …
$ WESTERN.REGION                 <chr> "FATAL", "0", "0", "0", "0", "0", "0", …
$ X.19                           <chr> "SERIOUS", "1", "1", "2", "0", "2", "2"…
$ X.20                           <chr> "NOINJURY", "0", "0", "0", "0", "0", "0…
$ X.21                           <chr> "OTHER", "0", "2", "4", "1", "1", "1", …

# Inspect the size of the dataset
# Get the dimensions of the dataset
dims = dim(accident_data)
obs = dims[1]
vars = dims[2]

# Print the values
cat("Number of observations:", obs, "\n")

Number of observations: 1644

cat("Number of variables:", vars, "\n")

Number of variables: 29

Answer

In the data there are 29 columns and 1644 rows, but 1643 of these are observations due to the first row containing header information.

Q1.2

Answer

Based on the data type selection tree, there are four data types in the data.

Metric Continuous: Dates.
1. Metric: Dates involve units of measurement (like time intervals), which makes them metric.
2. Continuous: Dates can be placed on a number line and have meaningful intervals (e.g., the difference between two dates can be measured in days, months, or years).
Metric Discrete: Accident counts.
1. Metric: Accident counts can be put on a number line (e.g. 0, 1, 2 accidents) and it has units (accidents).
2. Discrete: The accident count doesn’t come from measuring, it comes from counting.
Categorical Nominal: Region names.
1. Categorical: The region names cannot be put on a number line.
2. Nominal: There is no meaningful order to the names of the regions.
Categorical Ordinal: Accident types.
1. Categorical: The type of accident cannot be put on a number line.
2. Ordinal: We can put the accident types into a meaningful order based on severity, e.g. OTHER, NOINJURY, SERIOUS, FATAL.

Q1.3

# Count the number of regions in the data by selecting only columns containing the word
# REGION and then get the number of columns from this selection. 
# Filter columns with "REGION" in their names
regions = accident_data |> 
  dplyr::select(contains("REGION"))

# Get the number of columns in the slected data
num_regions = dim(regions)[2]

# Print the values
cat("Number of regions:", num_regions, "\n")

Number of regions: 7

# The data imports with two rows for the header and the Date values are in the first
# column called X.
# I just need to get the values from the 2nd to the last row in the first column.

# Extract the date values starting from the second row
date_values = accident_data$X[2:nrow(accident_data)]

# Convert to Date format (day/month/year)
date_values = dmy(date_values)

# Get the date range
date_range = range(date_values, na.rm = TRUE)

# Print the result
print(date_range)

[1] "2016-01-01" "2020-06-30"

Answer

The number of regions in the data is 7.
The time period covered by the data is from January 1st 2016 to June 30th 2020.

Q1.4

Answer

The variable FATAL represents accident that result in death. It is a count of how many people died in each region on a given date in car accidents. The variable SERIOUS represents accidents that result in serious injuries, but not death. It is a count of how many people were seriously injured in each region on a given date in car accidents. The difference between the variables is death. They both count car accidents, but FATAL records if death occurred. Visual inspection of the data shows the there are more SERIOUS accidents than FATAL.

Q2: Tidy data

Q2.1

# This code was provided with the question
cav_data_link <- 'car_accidents_victoria.csv' 
top_row <- read_csv(cav_data_link, col_names = FALSE, n_max = 1) 
second_row <- read_csv(cav_data_link, n_max = 1) 
 
column_names <- second_row %>%  
  unlist(., use.names=FALSE) %>%  
  make.unique(., sep = "__") # double underscore 
 
column_names[2:5] <- str_c(column_names[2:5], '0', sep='__') 
 
daily_accidents <-  
  read_csv(cav_data_link, skip = 2, col_names = column_names)

Answer

# Use top row to extract the region names
region_names = top_row |>
  dplyr::select(-X1) |> 
  unlist(use.names = FALSE) |> 
  discard(~ .x == "" | is.na(.x)) |> 
  unique()

print(region_names)

[1] "EASTERN REGION"                 "METROPOLITAN NORTH WEST REGION"
[3] "METROPOLITAN SOUTH EAST REGION" "NORTH EASTERN REGION"          
[5] "NORTHERN REGION"                "SOUTH WESTERN REGION"          
[7] "WESTERN REGION"

Q2.2

Answer

a.

Does each variable have its own column? No. Apart from the DATE column, all other columns are combinations of two variables, the accident type (FATAL, SERIOUS, NOINJURY, OTHER) and the region (as a number).
Does each observation have its own row? No. Each row is a date plus results (counts) for combinations of region and accident types. A single observation per row would be one date, one region, one accident type and the count.
Does each value have its own cell? Yes. The number of accidents (count) is in its own cell.

b.

# Pivot to long format
tidy_accidents = daily_accidents |>
  pivot_longer(
    cols = -DATE,
    names_to = "var",
    values_to = "accident_count"
  )

# Separate accident type and region index
tidy_accidents = tidy_accidents |> 
  separate(var, into = c("accident_type", "region_index"), sep = "__") |>
  mutate(region_index = as.integer(region_index))

# Map region_index to region names using region_names
tidy_accidents <- tidy_accidents |>
  mutate(region_name = region_names[region_index + 1]) # +1 because R is 1-based

How many pivot_wider operation do you need? None, the data is already in wide format.
How many pivot_longer operations do you need? One.
Explain the steps in detail.
- Step 1: Gather all columns except DATE into two columns called “var” and “accident_count”. Column “var” contains the original column names which is a combination of accident type and region. The “accident_count” columns contains the values from the original columns (i.e. the number of accidents).
- Step 2: Separate the values in the “var” column into two columns, “accident_type” (type of accident) and “region_index” (index of region). The “region_index” is converted into integers using the mutate function.
- Step 3: The last step is optional, but it takes the region_index and creates a column for the “region_name” by indexing the region_names list create in Q2.1.
Provide/print the head of the dataset.

head(tidy_accidents)

# A tibble: 6 × 5
  DATE      accident_type region_index accident_count region_name               
  <chr>     <chr>                <int>          <dbl> <chr>                     
1 1/01/2016 FATAL                    0              0 EASTERN REGION            
2 1/01/2016 SERIOUS                  0              1 EASTERN REGION            
3 1/01/2016 NOINJURY                 0              0 EASTERN REGION            
4 1/01/2016 OTHER                    0              5 EASTERN REGION            
5 1/01/2016 FATAL                    1              0 METROPOLITAN NORTH WEST R…
6 1/01/2016 SERIOUS                  1              7 METROPOLITAN NORTH WEST R…

c.

Are the variables having the expected variable types in R? No, not all variables have the expected type. The “DATE” columns needs to be converted to a Date, the “accident_type” column should be an ordered factor, “accident_count” should be an integer and region_name should be a factor.

tidy_accidents = tidy_accidents |>
  mutate(DATE = dmy(DATE))  |> 
  mutate(
    accident_type = ordered(accident_type,levels = c("OTHER", "NOINJURY",
                                                     "SERIOUS", "FATAL"))
    ) |> 
  mutate(accident_count = as.integer(accident_count)) |> 
  mutate(region_name = as.factor(region_name))

head(tidy_accidents)

# A tibble: 6 × 5
  DATE       accident_type region_index accident_count region_name              
  <date>     <ord>                <int>          <int> <fct>                    
1 2016-01-01 FATAL                    0              0 EASTERN REGION           
2 2016-01-01 SERIOUS                  0              1 EASTERN REGION           
3 2016-01-01 NOINJURY                 0              0 EASTERN REGION           
4 2016-01-01 OTHER                    0              5 EASTERN REGION           
5 2016-01-01 FATAL                    1              0 METROPOLITAN NORTH WEST …
6 2016-01-01 SERIOUS                  1              7 METROPOLITAN NORTH WEST …

d.

Are there any missing values? Yes, there are 4 missing values in the accident_count column.

cat("Number of missing observations per column:\n")

Number of missing observations per column:

# Count missing values per column
colSums(is.na(tidy_accidents))

          DATE  accident_type   region_index accident_count    region_name 
             0              0              0              4              0

# Get some summary statistics
summary(tidy_accidents)

      DATE             accident_type    region_index accident_count 
 Min.   :2016-01-01   OTHER   :11501   Min.   :0     Min.   : 0.00  
 1st Qu.:2017-02-14   NOINJURY:11501   1st Qu.:1     1st Qu.: 0.00  
 Median :2018-04-01   SERIOUS :11501   Median :3     Median : 0.00  
 Mean   :2018-04-01   FATAL   :11501   Mean   :3     Mean   : 1.44  
 3rd Qu.:2019-05-17                    3rd Qu.:5     3rd Qu.: 1.00  
 Max.   :2020-06-30                    Max.   :6     Max.   :33.00  
                                                     NA's   :4      
                         region_name  
 EASTERN REGION                :6572  
 METROPOLITAN NORTH WEST REGION:6572  
 METROPOLITAN SOUTH EAST REGION:6572  
 NORTH EASTERN REGION          :6572  
 NORTHERN REGION               :6572  
 SOUTH WESTERN REGION          :6572  
 WESTERN REGION                :6572

From the summary data above you can see the median in the accident_count is 0, the mean is 1.44 and the maximum accident_count is 33. The mean is higher than the median, potentially due to outliers. Therefore, I will use the median value to impute the missing counts as it is robust against outliers, it also retains the data being an integer type. Whilst, the crash data is also a time series I do not believe a froward fill or backward fill is appropriate here. The number of accident yesterday to tomorrow are unlikely to be related to today.

# Fix missing data in the count column using the median.
tidy_accidents <- tidy_accidents |>
  mutate(accident_count = if_else(is.na(accident_count),
                                  median(accident_count, na.rm = TRUE), accident_count))

# Check the missing count is now zero in all columns.
colSums(is.na(tidy_accidents))

          DATE  accident_type   region_index accident_count    region_name 
             0              0              0              0              0

Q3: Fitting distributions

For this question I need to create the “TOTAL_ACCIDENTS” data. As confirmed by the unit chair (22/9/25) this is the total number of accidents for each day in the dataset.

# Group and summarise the accident_count by date
total_accidents = tidy_accidents |> 
  group_by(DATE) |> 
  summarise(count = sum(accident_count), .groups = "drop")

Q3.1

Answer

Poisson distribution

# get total count
total_count = total_accidents$count

# Fitting a Poisson distribution
fit_pois = fitdist(total_count, "pois")

# View summary
summary(fit_pois)

Fitting of the distribution ' pois ' by maximum likelihood 
Parameters : 
       estimate Std. Error
lambda 40.32806  0.1566696
Loglikelihood:  -6565.159   AIC:  13132.32   BIC:  13137.72

# Plot diagnostic graphs
plot(fit_pois)

Negative binomial distribution

# Fitting a negative binomial distribution
fit_nb = fitdist(total_count, "nbinom")

# View summary
summary(fit_nb)

Fitting of the distribution ' nbinom ' by maximum likelihood 
Parameters : 
     estimate Std. Error
size 26.89578  1.5909547
mu   40.32640  0.2476714
Loglikelihood:  -6110.248   AIC:  12224.5   BIC:  12235.3 
Correlation matrix:
             size           mu
size 1.0000000000 0.0002372614
mu   0.0002372614 1.0000000000

# Plot diagnostic graphs
plot(fit_nb)

Q3.2

Answer

# Create a summary table
distribution_lik_comparison = tibble(
  Model = c("Poisson", "Negative Binomial"),
  LogLikelihood = c(fit_pois$loglik, fit_nb$loglik)
)
print(distribution_lik_comparison)

# A tibble: 2 × 2
  Model             LogLikelihood
  <chr>                     <dbl>
1 Poisson                  -6565.
2 Negative Binomial        -6110.

From the above log-likelihood values, the negative Binomial distribution has the higher (least negative) value, which means it fits the data better than the Poisson distribution, this is supported with the density plots produced for each distribution. This suggest that the accident count data likely exhibits over-dispersion (the variance is greater than the mean) as the negative Binomial distribution can handle data that exhibits over-dispersion. For a Poisson distribution, the variance is equal to the mean, making it harder to fit data with over-dispersion.

Q3.3

Answer

This question requires the total counts across regions grouped by accident type. It also requires the addition of a third distribution to assess. Although the data is discrete, I included the Normal distribution to explore how a continuous model might capture the overall shape and spread of accident counts, especially since other discrete alternatives like the Geometric distribution did not reflect the characteristics of the data well.

# Group and summarise the accident_count by date and accident type
total_accidents_by_type = tidy_accidents |> 
  group_by(DATE, accident_type) |> 
  summarise(count = sum(accident_count), .groups = "drop")

# Filter for SERIOUS accident types
serious_accidents = total_accidents_by_type |>
  filter(accident_type == "SERIOUS")

serious_counts = serious_accidents$count

# Filter for FATAL accident types
fatal_accidents = total_accidents_by_type |>
  filter(accident_type == "FATAL")

fatal_counts = fatal_accidents$count

# Fitting distributions to the SERIOUS data
fit_nb_ser = fitdist(serious_counts, "nbinom")
fit_pois_ser = fitdist(serious_counts, "pois")
fit_norm_ser = fitdist(serious_counts, "norm")

# Fitting distributions to the FATAL data
fit_nb_fat = fitdist(fatal_counts, "nbinom")
fit_pois_fat = fitdist(fatal_counts, "pois")
fit_norm_fat = fitdist(fatal_counts, "norm")

# Create a DataFrame manually with log-likelihoods
results_table_3_3 = data.frame(
  Distribution_name = c("Poisson", "Negative Binomial", "Normal",
                        "Poisson", "Negative Binomial", "Normal"),
  Accident_type = c("SERIOUS", "SERIOUS", "SERIOUS",
                    "FATAL", "FATAL", "FATAL"),
  Log_likelihood = c(
    fit_pois_ser$loglik,
    fit_nb_ser$loglik,
    fit_norm_ser$loglik,
    fit_pois_fat$loglik,
    fit_nb_fat$loglik,
    fit_norm_fat$loglik
  )
)

print(results_table_3_3)

  Distribution_name Accident_type Log_likelihood
1           Poisson       SERIOUS      -6225.577
2 Negative Binomial       SERIOUS      -5464.884
3            Normal       SERIOUS      -5356.787
4           Poisson         FATAL      -2010.458
5 Negative Binomial         FATAL      -2009.523
6            Normal         FATAL      -2242.277

I fitted three distributions, Poisson, Negative Binomial, and Normal to the TOTAL_ACCIDENTS data for SERIOUS and FATAL accident types. The goal was to assess which distribution best models the data by comparing their log-likelihood values.

For SERIOUS accidents, the Normal distribution had the highest log-likelihood (-5356.787), followed by the Negative Binomial (-5464.884), and then Poisson (-6225.577). This suggests that the Normal distribution may better capture the central tendency and spread of the data. However, since accident counts in accidents are discrete, the Negative Binomial is a better choice, although it yields a slightly lower log-likelihood.

For FATAL accidents, the best result was offered by the Negative Binomial (-2009.523), just edging out the Poisson (-2010.458), and the Normal lagged behind (-2242.277). This indicates that the Negative Binomial effectively models the over-dispersion and variability in fatal accident counts.

Overall, the Negative Binomial distribution consistently provides a strong fit across both accident types, striking a balance between statistical performance and suitability for discrete count data. The Normal distribution may be useful in exploratory analysis, but is less appropriate for modelling count-based outcomes.

Q4: Source weather data

To answer questions 4 and 5, I need to select a region. The unit chair confirmed this via email on 22/9/25. I have used the answer to question 7.1, which is the “METROPOLITAN SOUTH EAST REGION”.

Q4.1

Answer

For my data source I selected the NOAA Climate data because it was freely available, accessible from within R, has the data range I required, has the variables (temperature and precipitation) I require and comes in a form the is easy to work with within R.

Q4.2

Answer

For the weather station I have chosen Moorabbin airport as it is within the region of interest.

# Set some options
station_id = "ASN00086077"  # MOORABBIN AIRPORT 
start_date = "2015-12-02" # 30 days before the start of the accident data. Helps with Q5
end_date   = "2020-07-02" # 2 days after the accident data. Helps with Q5 

# Download data
noaa_data = ghcnd_search(stationid = station_id,
                         date_min = start_date, date_max = end_date)

# Combine tmin and tmax to get average temperature
# Merge tmin and tmax by date
temps = merge(noaa_data$tmin, noaa_data$tmax, by = "date", suffixes = c("_min", "_max"))

# Count missing values per column
cat("Number of missing observations in temperature:\n")

Number of missing observations in temperature:

colSums(is.na(temps))

     date    id_min      tmin mflag_min qflag_min sflag_min    id_max      tmax 
        0         0         1         0         0         0         0         0 
mflag_max qflag_max sflag_max 
        0         0         0

# Forward fill missing values for average temperature and precipitation.
# Here I have assumed that today's temperature a good approximation for tomorrow.
temps$tmin = na.locf(temps$tmin) 

# Calculate average temperature (in tenths of degrees C, so divide by 10)
temps = temps |>
  mutate(
    tavg = (tmin + tmax) / 2 / 10
  )
temps$tmin = temps$tmin / 10
temps$tmax = temps$tmax / 10

# Precipitation (in in tenths of millimeter, so divided by 10)
prcp = noaa_data$prcp
prcp$prcp = prcp$prcp / 10

# Count missing values per column
cat("\nNumber of missing observations in precipitation:\n")


Number of missing observations in precipitation:

colSums(is.na(prcp))

   id  prcp  date mflag qflag sflag 
    0     3     0     0     0     0

# Forward fill missing values for precipitation.
# Similar to temperature, I have assumed today's rainfall is a good approximation for
# tomorrow.
prcp$prcp = na.locf(prcp$prcp)

# Merge temperature and precipitation by date
weather_data = merge(temps[, c("date", "tmin", "tmax", "tavg")],
                     prcp[, c("date", "prcp")], by = "date", all = TRUE)

# Count missing values per column
cat("\nNumber of missing weather observations:\n")


Number of missing weather observations:

colSums(is.na(weather_data))

date tmin tmax tavg prcp 
   0    0    0    0    0

weather_data |>  
  ggplot(aes(x=date, 
             y=tavg)) + 
  geom_line(color='darkgreen') + 
  labs(
    title =  expression("Average Daily Temperature (" * degree * "C" * ")"),
    x = "Date",
    y = expression("Average Temperature (" * degree * "C" * ")")
  ) +
  theme(plot.title=element_text(hjust=0.5))

weather_data |>  
  ggplot(aes(x=date, 
             y=prcp)) + 
  geom_line(color='blue') + 
  labs(
    title = "Daily Precipitation (mm)",
    x = "Date",
    y = "Precipitation (mm)"
  ) +
  theme(plot.title=element_text(hjust=0.5))

Q4.3

Answer

# Get the dimensions of the dataset
dims = dim(weather_data)
obs = dims[1]
vars = dims[2]

# Print the values
cat("Number of observations:", obs, "\n")

Number of observations: 1675

There are 1675 rows in the local weather data.

# Get the date range
weather_date_range = range(weather_data$date, na.rm = TRUE)

# Print the result
print(weather_date_range)

[1] "2015-12-02" "2020-07-02"

The data covers the time period from December 12th 2015 to July 2nd 2020. This date range has been extend before and after the accident data range to accommodate rolling averages required in the answer to Question 5.

Q5: Heatwaves, preciptation and road accidents

Q5.1

Answer

The paper “The Excess Heat Factor: A Metric for Heatwave Intensity and Its Use in Classifying Heatwave Severity” by John R. Nairn and Robert J. B. Fawcett proposes a new index, the Excess Heat Factor (EHF), for monitoring and forecasting heatwaves in Australia. The EHF is designed to measure heatwave intensity in a way that is relevant to human health outcomes and can be applied consistently across Australia’s diverse climates. It achieves this by considering both long-term climate norms and short-term acclimatisation to recent temperatures.

The EHF is a measure of heatwave intensity calculated over a three-day period (TDP). It is formulated from two separate indices, called Excess Heat Indices (EHIs). The EHIs are the Significance Index (EHIsig) and the Acclimatisation Index (EHIaccl).

The EHIsig index measures the intensity of TDP relative to the location’s long-term climate. It is defined as the three-day-averaged Daily Mean Temperature (DMT) minus the Long-Term Threshold (T95) temperature threshold. A positive EHIsig indicates that the three-day period is unusually warm for that location. DMT is the simple average of the daily maximum and daily minimum temperatures, and T95 is the 95th percentile of the DMT, calculated from a long-term climatological record (e.g., 1971-2000) for a specific location.

The EHIaccl index measures how the temperature of a three-day period compares to the recent past, accounting for human adaptation. It is defined as the three-day-averaged DMT minus the average DMT of the preceding 30 days. A positive EHIaccl signifies that the three-day period is hotter than the recent past, suggesting a lack of acclimatisation.

The Excess Heat Factor (EHF) is the product of these two indices, with the condition that the acclimatisation index only amplifies the result if it is greater than 1. A heatwave is considered to be present only when the EHF is positive, which requires the significance index (EHIsig) to be positive.

Q5.2

Answer

# Calculate the Excess Heat Factor (EHF)

# Calculate the long-term 95th percentile (T95)
# The paper uses a 1971-2000 climatology period.
# Download data date from 1971 to 2000
noaa_data_1971_2000 = ghcnd_search(
  stationid = station_id,
  date_min = "1971-01-01",
  date_max = "2000-12-31"
)

# Combine tmin and tmax to get average temperature
# Merge tmin and tmax by date
temps_1971_2000 = inner_join(noaa_data_1971_2000$tmin, noaa_data_1971_2000$tmax,
                             by = "date", suffix = c("_min", "_max")) |>
  mutate(tavg = (tmin + tmax) / 2 / 10)

# Calculate the 95% percentile, ignoring and NA's
t95 = quantile(temps_1971_2000$tavg, probs = 0.95, na.rm = TRUE)
cat("Calculated T95 (95th percentile temperature) is:", round(t95, 2), "\u00B0C")

Calculated T95 (95th percentile temperature) is: 23.2 °C

# Calculate 3-day and 30-day rolling mean temperatures
# For 3-day DMT I use a 'left' alignment to match the paper's forward-looking formula
# for a three-day period (TDP) starting on day 'i' (T_i, T_{i+1}, T_{i+2}) page 233.
weather_data = weather_data |> 
  mutate(
      # 3-day average DMT
      dmt_3day_avg = rollmean(tavg, k = 3, fill = NA, align = "left"),
      # 30-day average DMT. Lag the temperature series before applying a 
      # trailing (right-aligned) rolling mean.
      dmt_30day_past_avg = rollmean(lag(tavg), k = 30, fill = NA, align = "right")
    )

# Calculate the Excess Heat Indices (EHI)
weather_data = weather_data |> 
    mutate(
      # Significance Index
      EHI_sig = dmt_3day_avg - t95,
      # Acclimatisation Index
      EHI_accl = dmt_3day_avg - dmt_30day_past_avg
    )

# Calculate the Excess Heat Factor (EHF)
# EHF is the product of the two indices.
# A heatwave is only present if EHF is positive, which requires EHI_sig > 0.
# Negative EHF values are set to 0 as their magnitude is not interpreted.
weather_data = weather_data |> 
    mutate(
      EHF = EHI_sig * pmax(1, EHI_accl),
      EHF = if_else(EHF < 0, 0, EHF)
    )

weather_data |> 
  ggplot(aes(x = date, y = EHF)) +
  geom_line(color="red", linewidth = 0.8) + 
  labs(
    title = "Excess Heat Factor (EHF)",
    subtitle = "Based on the methodology by Nairn and Fawcett (2015)",
    x = "Date",
    y = expression("Excess Heat Factor (" * degree * "C"^2 * ")"),
    linetype = "Threshold"
  )+
  theme(plot.title=element_text(hjust=0.5), plot.subtitle=element_text(hjust=0.5) )

Q6: Model planning

Q6.1

Answer

a.

The main goal of the model is to predict the daily number of road traffic accidents in a specific region of Victoria. This predictive model will be used for forecasting, enabling proactive resource management and public safety alerts.

b.

The model is highly relevant, as the number of accidents directly correlates with the demand for emergency services, such as ambulances, police, and fire brigades. Accurate prediction enables staff rostering, tactical deployment of units, and overall preparedness for particularly high-risk days as it relates to specific weather conditions.

c.

Potential users include emergency service planners, traffic management authorities (like VicRoads), public health officials, and government policy makers concerned with road safety.

Q6.2

Answer

a.

The plan is to model the relationship between various weather conditions (temperature and rainfall) and temporal factors (like day of the week, month) and the number of daily road traffic accidents.

b.

The response variable (\(Y\)) is the daily count of road traffic accidents in the selected region.

c.

The predictor variables will be:

Weather data: Maximum and minimum temperature and rainfall.
Heat-related metric: The Extreme Heat Factor (EHF).
Temporal factors: Month as a number.

d.

Yes. Weather data is forecast daily and measurements are usually available in real time or lagged by a day so so, making it ideal for predictive modeling. The temporal factors are known in advance. This allows the model to generate future predictions for operational planning. The EHF as formulated by John Nairn and Robert Fawcett needs two days forward of the calculation date, so any values used will also need to be 2 days behind the prediction.

e.

I will assume that the fundamental relationships between weather, driver behaviour, and accident risk will remain relatively stable in the short term. However, it’s a limitation to consider, as long-term trends like climate change, changes in vehicle technology, and new road infrastructure could alter these characteristics over a longer period.

Q6.3

Answer

The primary statistical methods will be Linear Models (LM) and Generalised Additive Models (GAM).

Linear Model: This will be used as a baseline model. It is simple to implement and interpret, and will help determine if there are any basic linear relationships between the predictors and the accident count.
Generalised Additive Model (GAM): This method will be used to improve the linear model because it relaxes the strict assumption of linearity. The relationship between weather variables and accidents is likely non-linear. A GAM can model these complex relationships using flexible smooth functions. Furthermore, since the response variable is a count and I have shown in Question 3 that the Negative Binomial distribution is better suited to the data, the GAM can be fitted using this distribution, which is more suitable for count data than the Normal distribution assumed by a standard linear model.

Q7: Model the number of road traffic accidents

Q7.1

set.seed(4)
selected_region = sample(region_names, 1)
selected_region

[1] "METROPOLITAN SOUTH EAST REGION"

Answer

My randomly selected region is “METROPOLITAN SOUTH EAST REGION”.

For this question I need to get the predictor variables together into a single DataFrame for this selected region.

region_totals = tidy_accidents |> 
  group_by(DATE, region_name) |> 
  summarise(count = sum(accident_count), .groups = "drop")

# Filter for the METROPOLITAN SOUTH EAST REGION
total_accidents_mse = region_totals |> 
  filter(region_name == "METROPOLITAN SOUTH EAST REGION")

total_accidents_mse = total_accidents_mse |> 
  dplyr::select(-region_name)

data = total_accidents_mse |> 
  mutate(
    weekday_num = wday(DATE, week_start = 1),  # Monday = 1
    month_num = month(DATE)                    # January = 1
  )

# Select only some of the columns from the weather_data
weather_selected <- weather_data |> 
  dplyr::select(date, tmin, tmax, tavg, prcp, EHF)  

# Merge using left_join to keep only rows from data
# This trims the weather data back to the same date range as the accidents
merged_df = data |> 
  left_join(weather_selected, by = c("DATE" = "date"))

Q7.2

Answer

I have interpreted linear model to mean linear regression not GLM. I have left the rainfall predictor for question 7.7.

Linear model

I fitted a linear model using lm() to predict the number of road traffic accidents (count) using weekday number, month number, maximum temperature (tmax), and minimum temperature (tmin) as predictors.

# Model 1: weekday, month, max and min temperature
lm_model1 <- lm(count ~ weekday_num + month_num + tmax + tmin, data = merged_df)
model1_results = augment(lm_model1)
summary(lm_model1)


Call:
lm(formula = count ~ weekday_num + month_num + tmax + tmin, data = merged_df)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.8626  -3.1626  -0.2735   3.0601  19.3361 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 14.18531    0.57039  24.869  < 2e-16 ***
weekday_num -0.36636    0.05818  -6.297 3.89e-10 ***
month_num    0.08205    0.03562   2.304 0.021371 *  
tmax         0.09106    0.02356   3.865 0.000116 ***
tmin        -0.08851    0.03453  -2.563 0.010460 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.716 on 1638 degrees of freedom
Multiple R-squared:  0.03602,   Adjusted R-squared:  0.03367 
F-statistic:  15.3 on 4 and 1638 DF,  p-value: 2.723e-12

The model summary shows the R-squared value is very low (~3.4%), indicating the linear model explains only a small portion of the variance in the accident counts.

Plot of fitted versus actuals

The model predicts values mostly between 12 and 18, regardless of the actual accident count, suggesting the model is not responsive to variation in the actual data. Actual accident counts vary widely (0 to 30), but the model doesn’t reflect this, indicating under-fitting. The plot does not following the expected diagonal trend (where fitted = actual). Here, the points are scattered horizontally, showing poor predictive accuracy. The fitted values do not closely follow the actual values, and there’s considerable scatter, suggesting poor predictive accuracy.

ggplot(data.frame(Actual =model1_results$count, Fitted = model1_results$.fitted),
       aes(x = Actual, y = Fitted)) +
  geom_point(alpha = 0.6, color = "darkgreen") +
  geom_abline(slope = 1, intercept = 0, linetype = "dashed", color = "red", size = 1.0) +
  labs(title = "Actual vs Fitted Values (Linear model) ", x = "Actual", y = "Fitted") +
  theme(plot.title=element_text(hjust=0.5))

Plot of residuals versus fitted

# Function for plotting residuals versus fitted
plot_residuals = function(model) {
  model_results = augment(model)
  model_results |> 
    ggplot(aes(.fitted, .resid)) +
    geom_point(alpha=0.5) +
    geom_hline(yintercept=0, color="red", linetype="dashed") +
    geom_quantile() +
    geom_smooth(colour="firebrick") +
    labs(title="Residuals vs Fitted (Linear model)", x="Fitted Values", y="Residuals") +
    theme(plot.title=element_text(hjust=0.5))
}

# Plot residuals
plot_residuals(lm_model1)

# Function to help plotting residuals versus feature
plot_residuals_v_feat = function(model, feature, label, sub_label, model_label) {
  model_results = augment(model)
  
  ggplot(model_results, aes_string(x = feature, y = ".resid")) +
    geom_point(alpha = 0.5) +
    geom_hline(yintercept = 0, color = "red", linetype = "dashed") +
    geom_quantile() +
    geom_smooth(colour = "firebrick") +
    labs(title = paste("Residuals vs", label, model_label), x = paste(label, sub_label),
         y = "Residuals") +
    theme(plot.title = element_text(hjust = 0.5))
}

Residuals vs Weekday number

plot_residuals_v_feat(model = lm_model1, feature = "weekday_num", label = "Weekday",
                      sub_label=" (1=Mon, ..., 7=Sun)", model_label="(Linear model)")

Residuals vs Month number

plot_residuals_v_feat(model = lm_model1, feature = "month_num", label = "Month",
                      sub_label=" (1=Jan, ..., 12=Dec)", model_label="(Linear model)")

Residuals vs Maximum temperature

plot_residuals_v_feat(model = lm_model1, feature = "tmax", label = "Maximum Temperature",
                      sub_label="", model_label = "(Linear model)")

Residuals vs Minimum temperature

plot_residuals_v_feat(model = lm_model1, feature = "tmin", label = "Minium Temperature",
                      sub_label="", model_label="(Linear model)")

Residuals versus fitted appear randomly scattered but with some spread, indicating that the linear model may not capture non-linear relationships or other structure in the data. Plots of residuals versus features show cyclic patterns for the day of the week and the month.

Based on the low R-squared value, residual patterns, and poor alignment between fitted and actual values, a linear model is insufficient for modeling the trend in accident counts.

Q7.3

Answer

# Weekday_num and month_num are cyclic so I have used the cyclic cubic spline "cc"
# and specific the wrap around knots
gam_nb = gam(
  count ~ s(weekday_num, bs="cc", k=7) + s(month_num, bs="cc", k=12) + s(tmax) + s(tmin),
  family=nb(link = "log"),
  data = merged_df,
  knots = list(weekday_num = c(1, 8),  # wrap from 7 to 1
               month_num = c(1, 13)    # wrap from 12 to 1
  ))
gam_nb_results = augment(gam_nb)
summary(gam_nb)


Family: Negative Binomial(34.53) 
Link function: log 

Formula:
count ~ s(weekday_num, bs = "cc", k = 7) + s(month_num, bs = "cc", 
    k = 12) + s(tmax) + s(tmin)

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) 2.640174   0.007836   336.9   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                 edf Ref.df Chi.sq p-value    
s(weekday_num) 4.667  5.000 171.23 < 2e-16 ***
s(month_num)   8.652 10.000  77.87 < 2e-16 ***
s(tmax)        2.533  3.242  16.85 0.00108 ** 
s(tmin)        1.007  1.013   5.68 0.01748 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.141   Deviance explained = 14.9%
-REML =   4809  Scale est. = 1         n = 1643

The GAM model improves upon the linear model by capturing non-linear relationships between predictors and accident counts. All smooth terms are statistically significant (p <0.05), some more than others (e.g. week_day compared to tmin) and the deviance explained is higher than in the linear model’s R-squared.

Plot of fitted versus actuals

This plot shows the plotted points now have a diagonal alignment closer to the actual=fitted line. This is an improvement compared to the linear model.

gam_nb_results$Fitted_transformed <- exp(gam_nb_results$.fitted)

ggplot(gam_nb_results, aes(x = count, y = Fitted_transformed)) +
  geom_point(alpha = 0.6, color = "darkgreen") +
  geom_abline(slope = 1, intercept = 0, linetype = "dashed", color = "red", size = 1.0) +
  labs(title = "Actual vs Transformed Fitted Values (GAM)", x = "Actual",
       y = "Fitted (transformed)") +
  theme(plot.title = element_text(hjust = 0.5))

Plot of residuals versus fitted

plot_residuals(gam_nb)

The residuals are scattered fairly evenly around the zero line, suggesting the model is not systematically over- or under-predicting, which is good. Most of the residuals fall within ±2, and the spread is symmetric, supporting the assumption that the model errors are random and unbiased.

The residual plot for the GAM shows no obvious patterns or violations of model assumptions. Residuals are randomly distributed around zero, indicating that the GAM provides a better fit than the linear model. This supports the use of a non-linear approach for modeling accident counts.

Residuals vs Weekday number

The residuals vs weekday plot shows no obvious structure or seasonal bias, indicating that the GAM model has effectively accounted for weekday variation in accident counts. This supports the adequacy of the model fit and suggests no major violations of model assumptions.

plot_residuals_v_feat(model = gam_nb, feature = "weekday_num", label = "Weekday",
                      sub_label=" (1=Mon, ..., 7=Sun)", model_label="(GAM)")

Residuals vs Month number

The residuals vs month plot shows no obvious structure or seasonal bias, indicating that the GAM model has effectively accounted for monthly variation in accident counts. This supports the adequacy of the model fit and suggests no major violations of model assumptions.

plot_residuals_v_feat(model = gam_nb, feature = "month_num", label = "Month",
                      sub_label=" (1=Jan, ..., 12=Dec)", model_label="(GAM)")

Residuals vs Maximum temperature

The residuals vs tmax plot shows no strong structure or trend, indicating that the GAM model has effectively accounted for the influence of maximum temperature on accident counts. This supports the adequacy of the model fit and suggests no major violations of assumptions related to this predictor.

plot_residuals_v_feat(model = gam_nb, feature = "tmax", label = "Maximum Temperature",
                      sub_label="", model_label="(GAM)")

Residuals vs Minimum temperature

The residuals vs tmin plot shows no strong structure or trend, indicating that the GAM model has effectively accounted for the influence of minimum temperature on accident counts. This supports the adequacy of the model fit and suggests no major violations of assumptions related to this predictor.

plot_residuals_v_feat(model = gam_nb, feature = "tmin", label = "Minium Temperature",
                      sub_label="", model_label="(GAM)")

Q7.4

Answer

AIC(lm_model1, gam_nb)

                df      AIC
lm_model1  6.00000 9765.983
gam_nb    20.18532 9566.777

Based on the AIC values, the GAM model with a Negative Binomial distribution (AIC = 9566.77) outperforms the linear model (AIC = 9765.983). This indicates that the GAM provides a better fit to the data while appropriately accounting for over-dispersion and non-linear relationships.

# Plot weekday
plot(gam_nb, select = 1, shade = TRUE, main = "Weekday",
     xlab = "Weekday (1=Mon, ..., 7=Sun)", ylab = "Effect on log(count)")

# Plot month
plot(gam_nb, select = 2, shade = TRUE, main = "Month",
     xlab = "Month (1=Jan, ..., 12=Dec)", ylab = "Effect on log(count)")

# Plot maximum temperature
plot(gam_nb, select = 3, shade = TRUE, main = "Maximum temperature",
     xlab = "Temperature (\u00B0C)", ylab = "Effect on log(count)")

# Plot minimum temperature
plot(gam_nb, select = 4, shade = TRUE, main = "Minimum temperature",
     xlab = "Temperature (\u00B0C)", ylab = "Effect on log(count)")

The smooth term for weekday reveals a weekly pattern in road traffic accidents, with highest counts on Fridays, and lowest counts on Sundays. This suggests that weekday is a meaningful predictor, likely capturing weekly driving conditions or travel behavior.

The smooth term for month reveals a seasonal pattern in road traffic accidents, with higher counts in late summer and late winter, and lower counts in autumn and early spring. This suggests that month of the year is a meaningful predictor, likely capturing seasonal driving conditions, weather, or travel behavior.

The smooth term for tmax suggests that accident counts tend to increase with rising temperatures up to around 30°C. This could reflect increased road usage or riskier driving conditions in warmer weather. However, the effect plateaus at very high temperatures, possibly due to behavioral changes (e.g., fewer people driving in extreme heat).

The smooth term for tmin indicates that lower minimum temperatures are associated with increased road traffic accidents. This could reflect hazardous driving conditions such as frost, fog, or reduced visibility during colder periods.

Q7.5

Answer

Residuals were analyzed from the GAM model fitted using a Negative Binomial distribution and log link, with smooth terms for weekday_num, month_num, tmax, and tmin. The residuals vs fitted values plot shows residuals scattered fairly evenly around zero, with no clear trend or curvature. Most residuals fall within ±2, and the spread appears symmetric.

plot(residuals(gam_nb, type = "deviance"), type = "l",
     main = "Residuals Over Time", ylab = "Deviance Residuals", xlab = "Time Index")
abline(h = 0, col = "red", lty = 2)

acf(residuals(gam_nb, type = "deviance"), main = "ACF of Residuals")

The residuals over time plot shows noticeable fluctuations and clustering, suggesting that the residuals are not entirely random. Combined with the ACF plot, this indicates the presence of autocorrelation and potential un-modelled temporal structure. Further refinement of the model, such as including lagged predictors or additional time-based features, may help address this. The drop in residuals towards the end of the time series is during the COVID-19 period when Victoria had lock down and restrictions on travel.

The ACF plot of residuals shows significant autocorrelation at lag 0 and some early lags, as indicated by vertical bars exceeding the 95% confidence bounds. This suggests that the residuals are not entirely independent and that the model may not have fully captured the temporal structure in the data. Further refinement, such as including lagged predictors or temporal smoothing, may be necessary to improve model fit.

Q7.6

Answer

gam_nb_ehf = gam(
  count ~ s(weekday_num, bs="cc", k=7) + s(month_num, bs="cc", k=12) 
          + s(tmax) + s(tmin) + s(EHF),
  family=nb(link = "log"),
  data = merged_df,
  knots = list(weekday_num = c(1, 8),  # wrap from 7 to 1
               month_num = c(1, 13)    # wrap from 12 to 1
  ))

summary(gam_nb_ehf)


Family: Negative Binomial(34.545) 
Link function: log 

Formula:
count ~ s(weekday_num, bs = "cc", k = 7) + s(month_num, bs = "cc", 
    k = 12) + s(tmax) + s(tmin) + s(EHF)

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) 2.640139   0.007836   336.9   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                 edf Ref.df  Chi.sq  p-value    
s(weekday_num) 4.667  5.000 171.973  < 2e-16 ***
s(month_num)   8.636 10.000  76.264  < 2e-16 ***
s(tmax)        2.311  2.975  17.579 0.000528 ***
s(tmin)        1.005  1.010   5.424 0.020132 *  
s(EHF)         1.459  1.785   1.248 0.383222    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.141   Deviance explained = 14.9%
-REML = 4812.2  Scale est. = 1         n = 1643

AIC(gam_nb, gam_nb_ehf)

                 df      AIC
gam_nb     20.18532 9566.777
gam_nb_ehf 22.29667 9569.528

Adding EHF to the GAM model did not improve model fit. The AIC increased slightly (from 9566.777 to 9569.528), and the smooth term for EHF was not statistically significant (p = 0.3832). Therefore, EHF does not appear to be a useful predictor for road traffic accident counts in this context.

Q7.7

Answer

gam_nb_prcp = gam(
  count ~  s(weekday_num, bs="cc", k=7) + s(month_num, bs="cc", k=12)
         + s(tmax) + s(tmin)+ s(prcp),
  family=nb(link = "log"),
  data = merged_df,
  knots = list(weekday_num = c(1, 8),  # wrap from 7 to 1
               month_num = c(1, 13)    # wrap from 12 to 1
  ))

summary(gam_nb_prcp)


Family: Negative Binomial(34.838) 
Link function: log 

Formula:
count ~ s(weekday_num, bs = "cc", k = 7) + s(month_num, bs = "cc", 
    k = 12) + s(tmax) + s(tmin) + s(prcp)

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) 2.640026   0.007827   337.3   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                 edf Ref.df  Chi.sq p-value    
s(weekday_num) 4.666  5.000 170.135 < 2e-16 ***
s(month_num)   8.677 10.000  80.537 < 2e-16 ***
s(tmax)        2.680  3.426  21.199 0.00020 ***
s(tmin)        1.003  1.006   6.933 0.00854 ** 
s(prcp)        1.048  1.094   4.329 0.03953 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.143   Deviance explained = 15.1%
-REML = 4810.7  Scale est. = 1         n = 1643

Comparsion of AIC values

AIC(gam_nb, gam_nb_prcp)

                  df      AIC
gam_nb      20.18532 9566.777
gam_nb_prcp 22.07495 9565.361

EHF was tested as a predictor but did not improve model fit, as indicated by a higher AIC and a non-significant smooth term. To explore alternatives, precipitation (prcp) was added to the model. It improved the fit marginally, with a lower AIC (9565.361) and a significant effect (p = 0.0395). Due to the lack of additional weather data for Moorabbin Airport, no further predictors could be tested. Based on available data, temperature variables (tmax and tmin) and precipitation (prcp) are the most predictive weather features for road traffic accidents.

Q8

Project Reflection Report

This report reflects on the statistical modelling of road traffic accidents, addressing potential model improvements, the handling of common data issues, and an overall assessment of the analysis objectives.

Q8.1: Additional data for model improvement

The current model relies on weather and time data for its forecast. To make it more predictive in value and useful in the real world, some additional sources of data might be included:

Traffic Volume Information: The traffic volume on the road is one determinant of the likelihood of accidents. Adding traffic loop detector data or GPS mobility data would provide a direct measure of risk exposure. A holiday with little traffic on a wet day, for example, might have a different accident risk than a wet day with heavy commuter traffic.
Public Events and Holidays: Big sporting events, festivals, and concerts produce big deviations in traffic volumes and driver behavior. An indicator variable for such an event would be capable of modeling these such abnormal spikes in demand. On the same principle, it would be preferable to have public and school holiday indicator variables included directly instead of including month effects.
Road Conditions and Infrastructure: Information regarding roadworks, diversions, road condition, and blackspots where accidents are known to occur can be useful predictors. Some of these will be unchanging, but information regarding temporary roadworks will often be present and extremely relevant.
Additional Weather Metrics: In addition to temperature, visibility is also crucial, as poor visibility due to fog or heavy precipitation may increase accident risk. Wind speed and gusts can significantly impact vehicle control, particularly for larger or lighter vehicles. Cloud cover and solar radiation significantly impact visibility and glare, especially during sunrise or sunset. Including these variables helps capture the complex ways weather impacts driving safety.

Q8.2: Achievement of analysis objectives

Yes, the analyses have successfully addressed the objective of predicting the daily number of road traffic accidents in a selected region of Victoria using weather and temporal data. The goal was to develop a model that supports emergency service planning and public safety forecasting by identifying patterns in accident risk based on forecastable variables.

The first baseline linear model helped identifying statistically significant predictors, including maximum and minimum temperatures, as well as the week day and month. However, the model explained only a small portion of the variance (adjusted R-squared of approximately 0.034), indicating that a linear approach was insufficient to account for the data.

To improve predictive performance, a Negative Binomial GAM was fitted. This model captured non-linear relationships and significantly improved the fit, with a higher adjusted R-squared (approximately 0.141), greater deviance explained (approximately 14.9%), and a lower AIC. The importance of the temperature, weekday and month predictors was confirmed through statistical significance.

Additional predictors were explored to make the model more precise. The Extreme Heat Factor (EHF) was tested but failed to improve the model, as indicated by a larger AIC and a non-significant smooth term. Precipitation was also attempted and was able to improve upon the model, with an decreased AIC (9565.361 vs. 9566.777) and significant effect (p = 0.03953). Due to limited weather data availability for Moorabbin Airport, no further predictors could be tested.

While the percentage of deviance explained is modest, the modelling is still a success for several reasons:

Real-world accident data is inherently noisy and influenced by many unobserved factors, such as driver behaviour, traffic volume, and road conditions.
The model identified statistically significant and interpretable relationships using forecastable variables.
It improved upon the baseline model and demonstrated that temperature, weekday and month are meaningful predictors.
The model is practical for short-term forecasting, aligning with the original objective of supporting emergency service planning.

Q8.3: Handling missing values

If the dataset contained missing values, several methods could be employed to address the issue, ranging from simple to complex. The choice of method depends on the extent and nature of the value that is missing (the missingness).

Complete Case Analysis or Listwise Deletion: It is the simplest method, involving removal of any row that has a missing value[1]. If the data is missing completely at random (MCAR), then listwise deletion “produces unbiased estimates of means, variances and regression weights” [1]. It the data is not MCAR can significantly reduce statistical power and introduce bias. The main disadvantage of listwise deletion is the loss of data as the entire case (row) is removed.
Single Imputation: In this approach, missing data is replaced by a single reasonable substitute [1]. Some common methods of selecting an acceptable substitute include replacing by the mean, median, or mode of the variable, adopting forward or backward filling methods[2]. Another sophisticated technique is regression imputation [1], wherein a regression model for imputation of the missing values is developed from other available variables.
Multiple Imputation (MI): MI is known to be very effective and “accepted as the best general method to deal with incomplete data in many fields”[1]. Instead of replacing a single value for missing observations, MI creates several plausible values for every missing entry, thus creating several complete data sets. Each of these imputed data sets is analysed for results that are then combined using existing guidelines (e.g., Rubin’s rules)[1]. This approach correctly takes into account the statistical uncertainty of the missing data such that greater precision of standard error and confidence intervals is obtained.

In this work, the dataset contained a small number of missing values that required handling before analysis. Several methods were considered to address this incomplete data. Given the extremely small proportion of missing traffic accident data (less than 0.25%), median imputation was a pragmatic and robust choice that avoids the unnecessary complexity of multiple imputation. For the missing temperature data, forward filling was used to preserve the temporal context, as the temperature from the previous day is a more logical estimate for a time-series than a simple statistical average of the entire dataset.

Q8.4: Tackling over-fitting from explanatory variables

Over-fitting occurs when a model captures noise or random fluctuations in the training data, resulting in poor generalisation to new data. In the context of Generalised Additive Models (GAMs), over-fitting can arise from using too many explanatory variables or overly flexible smooth terms.

To manage an excessive number of explanatory variables in a GAM and prevent over-fitting, two primary, complementary strategies can be employed: automatic feature selection via shrinkage smoothers and explicit model selection using information criteria, such as AIC.

Automatic Feature Selection (via Shrinkage): This is the most integrated approach. By using special “shrinkage” smoothers (e.g., by setting select=TRUE in R’s mgcv package), you introduce a penalty that can shrink the smooth functions of irrelevant variables completely to zero [3],[4]. This effectively performs automatic feature selection during the model fitting process, allowing you to include many candidate variables and let the model determine which ones are important.

Model Comparison and Selection (via AIC): The Akaike Information Criterion (AIC) is a widely used tool for balancing model fit and complexity. AIC penalises models with more parameters, helping to avoid over-fitting by favouring simpler models that still explain the data well [5]. You can perform a stepwise variable selection process by fitting models with different subsets of variables and choosing the model with the lowest AIC. Cross-validation with an error metric such as RMSE can be used as an alternative to AIC, but it would be more computationally expensive.

By applying these strategies, using shrinkage smoothers for automatic selection and performing manual elimination you can effectively and justifiably reduce the number of explanatory variables in your GAM to create a simpler and robust model.

In this work, only the model comparison and selection strategy using AIC for comparison of models was employed.

References

[1] S. van Buuren, Flexible Imputation of Missing Data, Second Edition. Second edition. | Boca Raton, Florida : CRC Press, [2019] |: Chapman and Hall/CRC, 2018. doi: https://doi.org/10.1201/9780429492259.

[2] H. Wickham, R. François, L. Henry, K. Müller, and D. Vaughan, “dplyr: A Grammar of Data Manipulation,” dplyr.tidyverse.org, 2025. https://dplyr.tidyverse.org

[3] S. Wood, “Help for package mgcv,” R-project.org, 2017. https://cran.r-project.org/web/packages/mgcv/refman/mgcv.html#gam (accessed Sep. 26, 2025).

[4] S. N. Wood, Generalized additive models : an introduction with R. Boca Raton Etc.: Crc Press - Taylor &Francis Group, 2017.

[5]J. E. Cavanaugh and A. A. Neath, “The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements,” Wiley Interdisciplinary Reviews: Computational Statistics, vol. 11, no. 3, pp. 1–11, Mar. 2019, doi: https://doi.org/10.1002/wics.1460.